Circles, Ellipses and Cylinders
Circles in Perspective
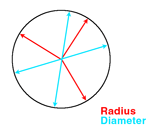
A circle is a shape that has all of its points on it the same distance from its center. The distance across a circle through the center is called the diameter. The radius of a circle is the distance from the center of a circle to any point on the circle. When viewed straight on, a circle will appear as a circle... as described above. Viewed at any other angle, a circle appears as an ellipse ...or if viewed edge-on, it appears as a straight line. |
 |
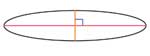
| An ellipse has a long, or major axis... a line drawn through the ellipse that is longer than any other line you can draw through the ellipse and which divides the ellipse across the longest dimension... in a horizontal ellipse, the long axis is horizontal. |  |
| An ellipse also has a short or minor axis which divides the ellipse into two equal halves across the narrowest dimension... which, in a horizontal ellipse, is a vertical line. |
 |
| The long and short axes are always perpendicular to each other... |  |
| No matter how squished the ellipse may be... |  |
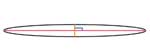| And no matter at what angle... the long and short axes are always perpendicular to each other |  |
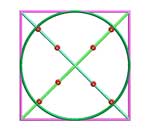
| A circle can be inscribed in a square. Notice that the circle touches the square at the midpoint of each side |  |
| and that the square and the circle have the same center point (as indicated by the crossing diagonals). |  |
| I divided each half of the diagonal lines into thirds... the circle almost passes through the outer marks |  |
| This is true in perspective as well. |  |
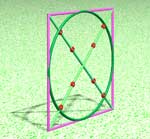If you draw a square in perspective, you can inscribe a circle in perspective within that square.1. Draw the square in perspective
|
 |
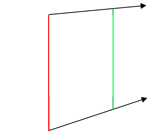| Find the center of the square using two diagonal lines, corner to corner. |  |
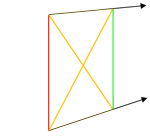Draw a vertical line through the center-point. Run a line through the center of the square toward the vanishing point. |
 |
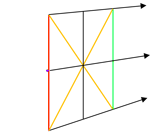| Make marks on the diagonal lines approximately 1/3 in from the corners. |  |
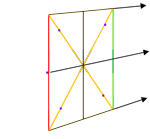| Sketch the ellipse connecting points 1 through 8 and back to 1. |  |
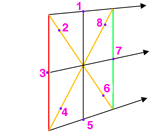Cylinders in Perspective |
|
| This is a cylinder |  |
If you look straight down at the top of a cylinder, it’s a circle. |
 |
| But if you look at its top at an angle, you see it as an ellipse. |  |
| The taller this cylinder becomes... the narrow the ellipse becomes |  |
| Until it reaches the height of your eye level, the horizon, at which point you see it as a straight line |  |
| When it's above your eye level, it again becomes an ellipse... although you can't see the entire ellipse... |  |
| When an ellipse is further away from the horizon, it becomes more open... the bottom of the cylinder is further below the horizon than its top, so it's even more open than the top. |  |
| Not only do cylinders have long and short axes on each of the elliptical ends, but cylinders also have axles... the short axis and the axle ALWAYS line up with each other... |  |
 |
 |
M.C.Escher |
Victor Vasarely |
 |
Claude Monet |
Robert Hubert |
 |
Assignments
Assume your eyes are 5' above the ground for all assignments and tests in this course, unless otherwise specified. |
|
LIGHTLY draw all lines in pencil, then ink the horizon and objects... leave the guidelines in pencil.On separate, 4 1/2" x 6" pieces of bristol board, draw the following:
|
|
| 1. Draw a Two Point Perspective Square on its edge and inscribe a perspective circle (an ellipse) within it... leave all guidelines and marks in pencil... emphasize the circle, square, and horizon line with ink. |  |
| 2. Draw a vertical Cylinder... be sure the top is visible as an ellipse. Leave the guidelines used to construct the cylinder and label them: Horizon, Long Axis, Short Axis, Axle, Ellipse. Show the bottom ellipse also (pretend the cylinder is transparent)! |
|
| Draw a cylinder lying on the ground... going off into the distance. Leave the guidelines used to construct the cylinder: Horizon, Vanishing Point, Long Axis, Short Axis, Axle, Ellipse. You don't have to label them. |
|
